【算法趣题】Q10轮盘的最大值

　　作者：简单的happy Python爱好者社区专栏作者
博客专栏：简单的happy 前言
【算法趣题】是来自图灵程序设计丛书绝云译的《程序员的算法趣题》，游戏问答书中是用Ruby实现的。这里是用python来实现。
问题描述
轮盘是机轮盘赌博会或者运气的游戏，几乎没有人可以操控赔率。不论您如何下注，赢得赌注的几率都是相对一定的，【算法趣题】Q10轮盘的最大值这是您无法改变的。
轮盘一般分两种：美式和欧式。美式有零位和双零位，而欧式则只有零位。前者赌场的优势为5.26%，而后者仅有2.7%。因此欧式轮盘将是更好的选择。
下面我们要找出在这些规则下，“连续n个数字的和”最大的位置。
举个例子，当n=3时，按照欧式规则得到的最大的组合是36,11,30这个组合，和为77；而美式规则下则是24,36,13这个组合，得到的和为73.（图中所示轮盘为欧式规则的轮盘，注意轮盘是圆形的）





欧式规则:
0,32,15,19,4,21,2,25,17,34,6,27,13,36,11,30,8,23,10,5,24,16,33,1,20,14,31,9,22,18,29,7,28,12,35,3,26

美式规则：
0,28,9,26,30,11,7,20,32,17,5,22,34,15,3,24,36,13,1,00,27,10,25,29,12,8,19,31,18,6,21,33,16,4,23,35,14,2
当 2 ≤ n ≤ 36时，求连续n个数之和最大的情况，并找出满足条件“欧式规则下的和小于美式规则下的和”的n的个数。
思路
我们先来考虑连续n个数之和最大的情况。我们用数组来表示轮盘的数字排布，比如欧式规则为：
European = [0,32,15,19,4,21,2,25,17,34,6,27,13,36,11,30,8,23,10,5,24,16,33,1,20,14,31,9,22,18,29,7,28,12,35,3,26]
美式规则为：

American = [0,28,9,26,30,11,7,20,32,17,5,22,34,15,3,24,36,13,1,00,27,10,25,29,12,8,19,31,18,6,21,33,16,4,23,35,14,2]
假如n=3，考虑到转盘是圆的，用数组表示的话，数组要扩充2（n-1）位，扩充的2位就是数组的前两位。数组的求和可以用sum。





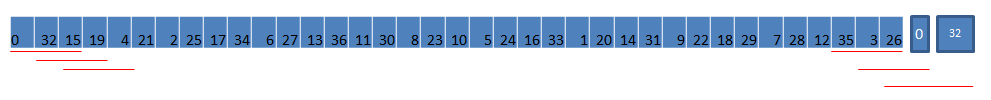
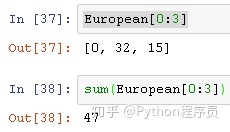
European 数组中的前3位可表示为 European[0: 3]，对这3位求和，即sum(European[0: 3])





数组添加元素，则使用append.

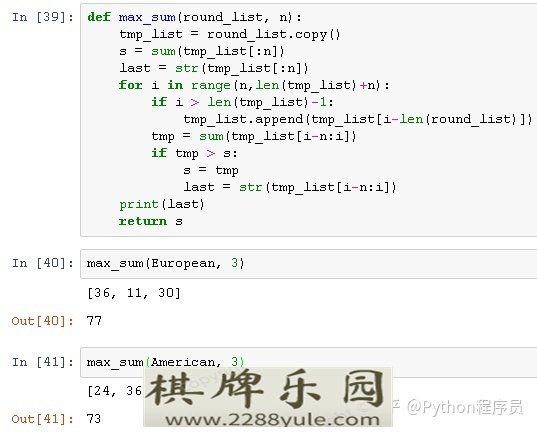
python3实现
def max_sum(round_list, n): tmp_list = round_list.copy() s = sum(tmp_list[:n]) last = str(tmp_list[:n]) for i in range(n,len(tmp_list)+n): if i len(tmp_list)-1: # 如果i超过原数组的长度，就要添加元素 tmp_list.append(tmp_list[i-len(round_list)]) tmp = sum(tmp_list[i-n:i]) if tmp s: s = tmp last = str(tmp_list[i-n:i]) # print(last) return s European = [0,32,15,19,4,21,2,25,17,34,6,27,13,36,11,30,8,23,10,5,24,16,33,1,20,14,31,9,22,18,29,7,28,12,35,3,26] American = [0,28,9,26,30,11,7,20,32,17,5,22,34,15,3,24,36,13,1,00,27,10,25,29,12,8,19,31,18,6,21,33,16,4,23,35,14,2] count = 0 for n in range(2,37): if max_sum(European, n) max_sum(American, n): count = count + 1 print(count) 答案为9。


可以来验证下，当n=3时，组合对不对。







到此为止，第一章入门篇共10个题，断断续续中完成了。接下来就是第二章初级篇了。游戏问答